Bio

I am a research scientist at the Robotics and AI Institute. My work combines machine learning, optimization, and computer vision to enhance robot capabilities in manipulation and locomotion. My goal is to bridge theoretical foundations with practical algorithmic solutions to enable robots to achieve human-level capabilities in whole-body manipulation within real-world environments.

Previously, I focused on developing fast optimization algorithms for simulation, planning, and control of robotic systems. I also designed and implemented differentiable physics tools for trajectory tracking, planning, and reinforcement learning tasks in robotic locomotion and manipulation. Additionally, I developed optimization algorithms that enable game-theoretic reasoning for autonomous vehicles.

Portfolio

Learning from planner demonstrations

With Jacta, we combined reinforcement learning with sampling-based algorithms to solve contact-rich manipulation tasks. While sampling-based planners can quickly find successful trajectories for complex manipulation tasks, the solutions often lack robustness. We leveraged a reinforcement learning algorithm to enhance the robustness of a set of planner demonstrations, distilling them into a single policy.

Unified collision detection and contact dynamics

With Silico, we unified collision detection and contact dynamics into a single optimization problem. With this novel formulation, we can smoothly differentiate through contact dynamics for objects of arbitrary shapes. Previous differentiable physics formulations were limited to simple shape primitives.

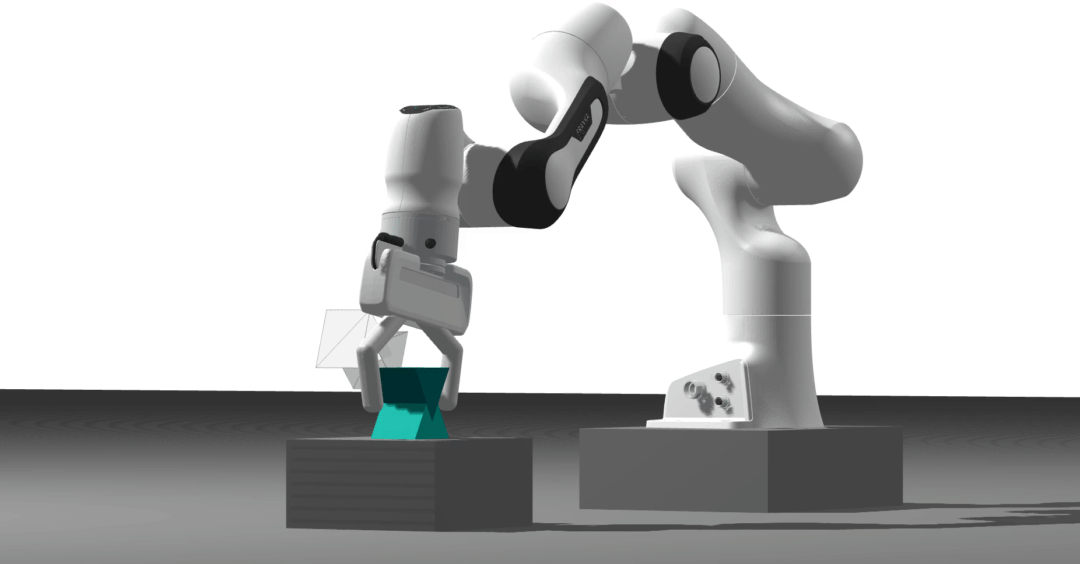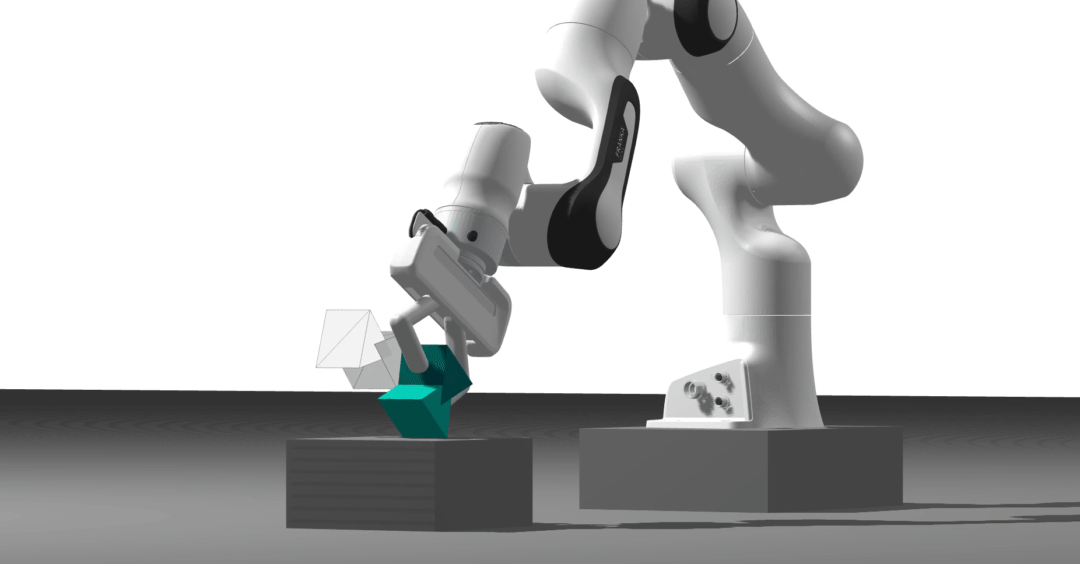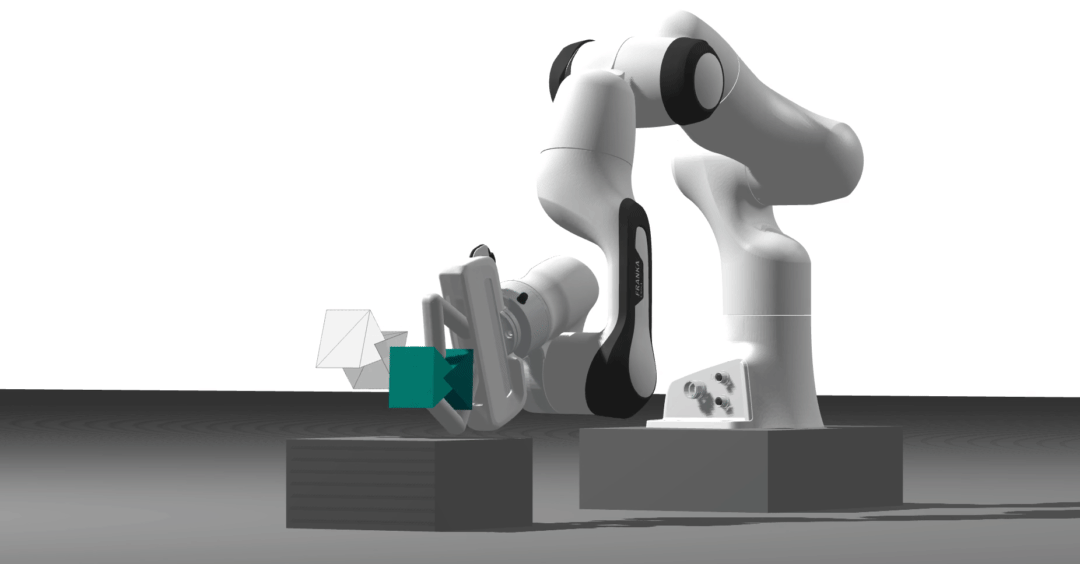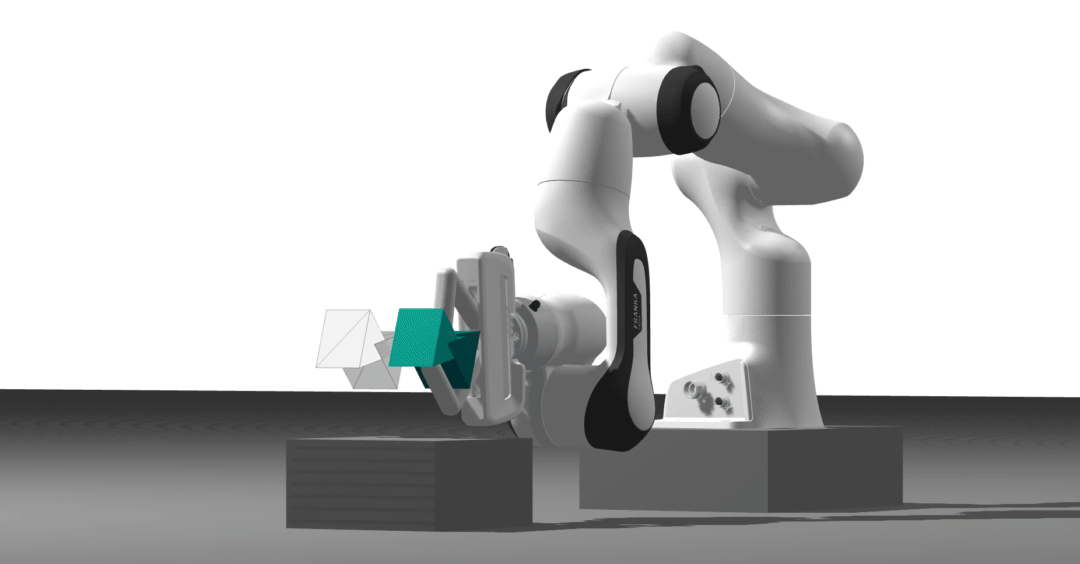
Differentiable physics engine

With Dojo, we took a physics- and optimization-first approach to address some of the limitations of the current physics engines. In particular, we can provide informative gradients through contact dynamics. Contrary to simulators relying on soft-contact models, Dojo can simulate hard contact interactions. Additionally, it does not need to approximate the friction cone to simulate sliding behavior.

Simulating neural objects contact interactions

We proposed a simple approach to neural object contact simulation. By augmenting a neural object with dynamics properties such as mass, inertia, coefficient of friction, we can simulate the object interaction with the environment, other objects or even oter neural objects.

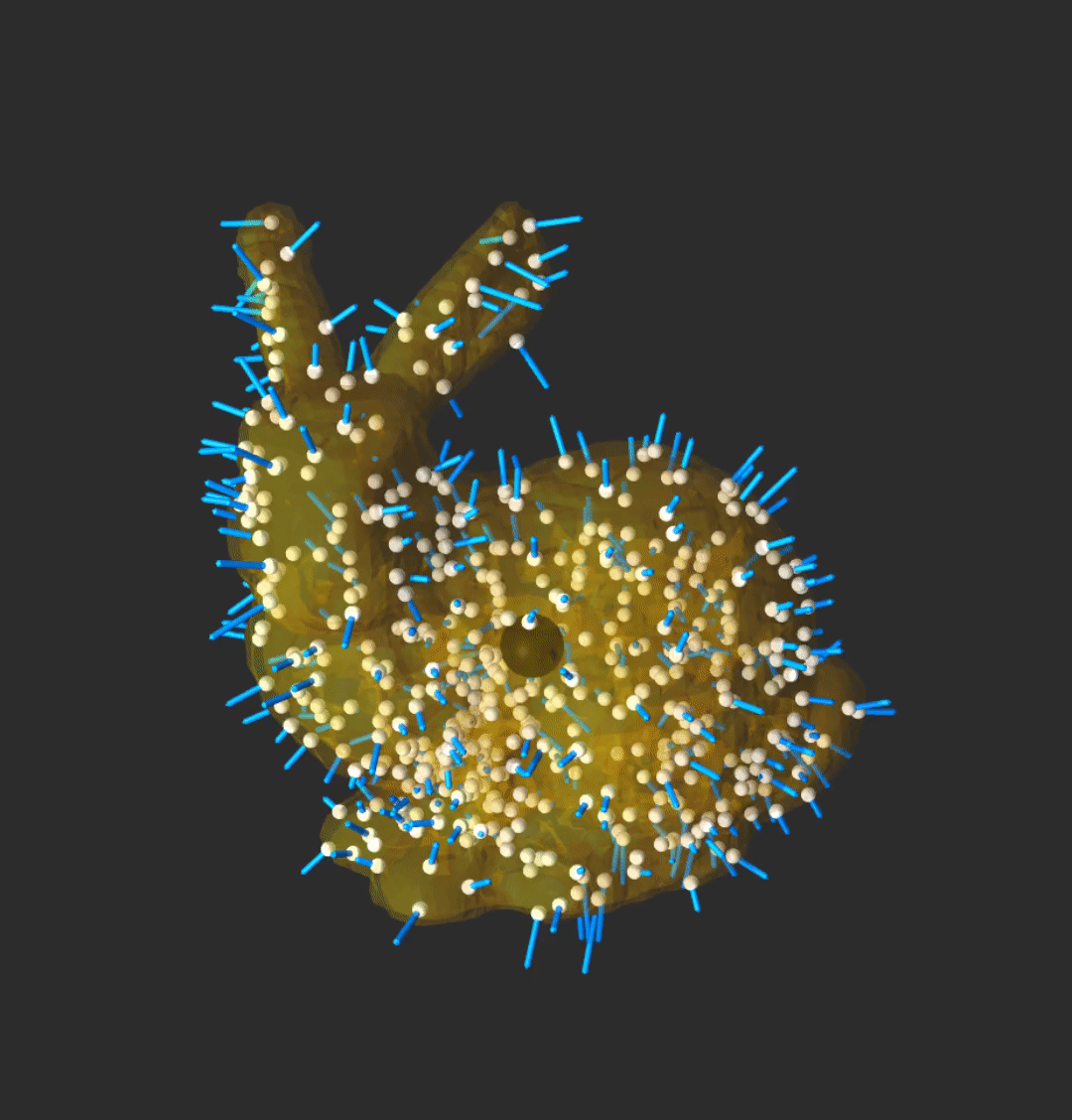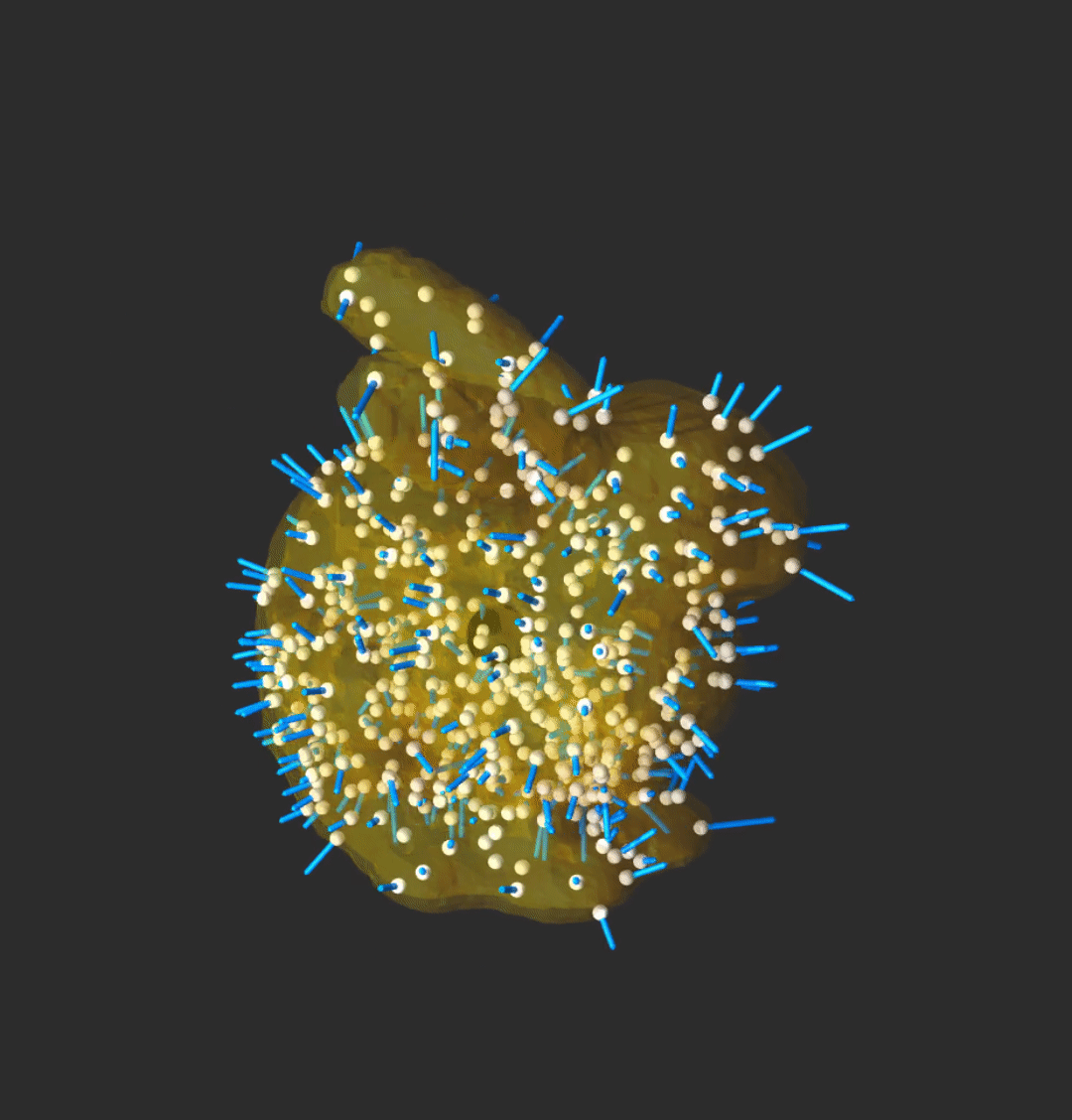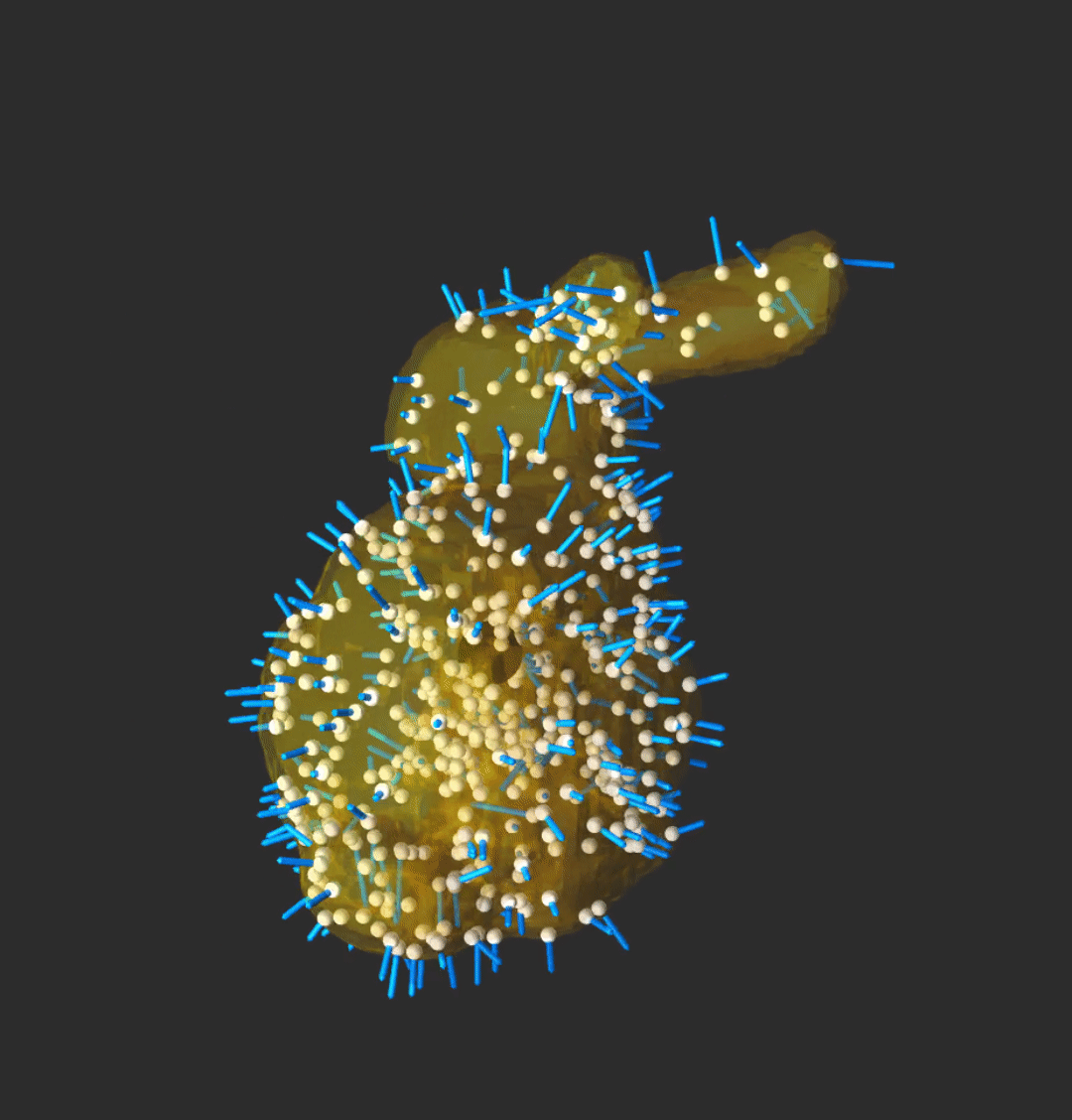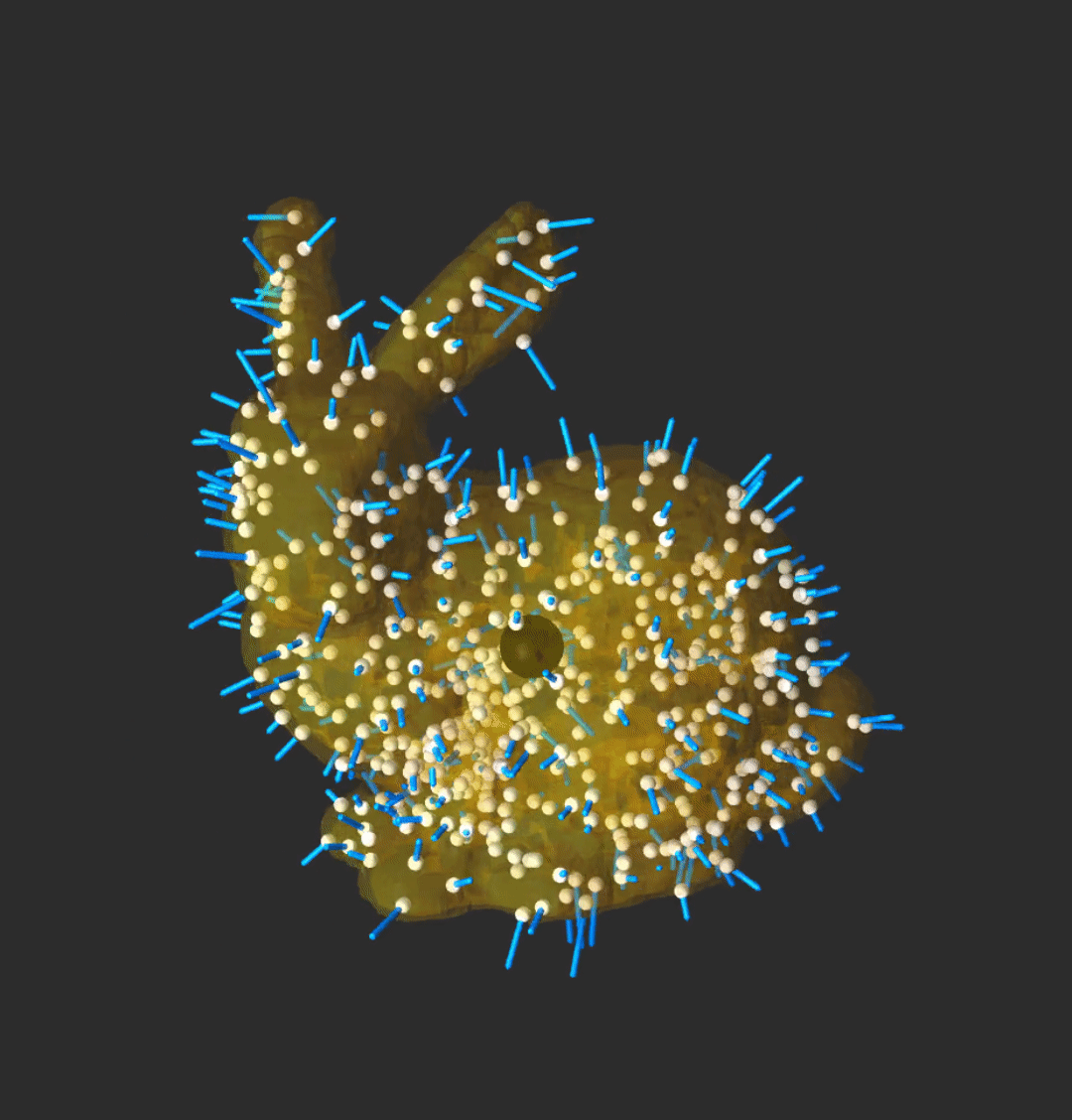
Optimizing through contact

We leveraged differentiable contact simulation for control through contact. We embedded a differentiable physics engine into an online optimization pipeline.

Learning Objective Functions

We coupled an online estimation technique and a fast dynamic game solver to allow an autonomous driving vehicle to optimize its trajectory while learning the objective functions of the cars in its surroundings. It allows the autonomous vehicle to quickly identify the desired speed, desired lane and aggresiveness level of the vehicles it is interacting with. This gained information further improves the trajectory prediction ability of the autonomous vehicle.

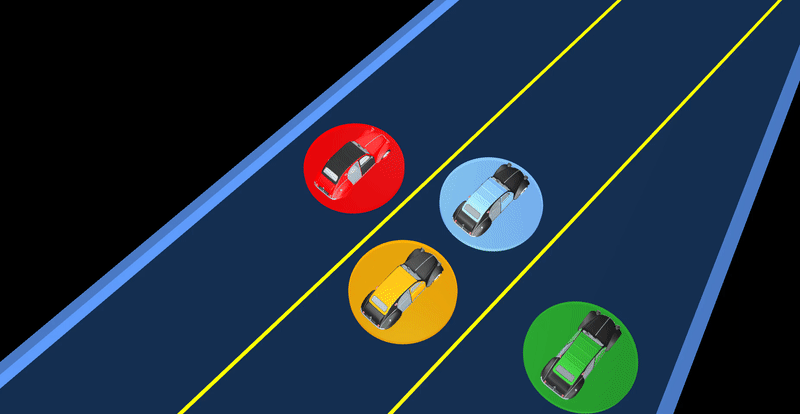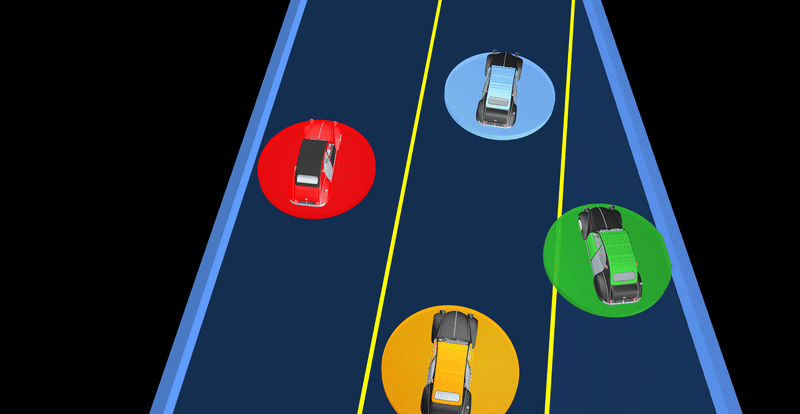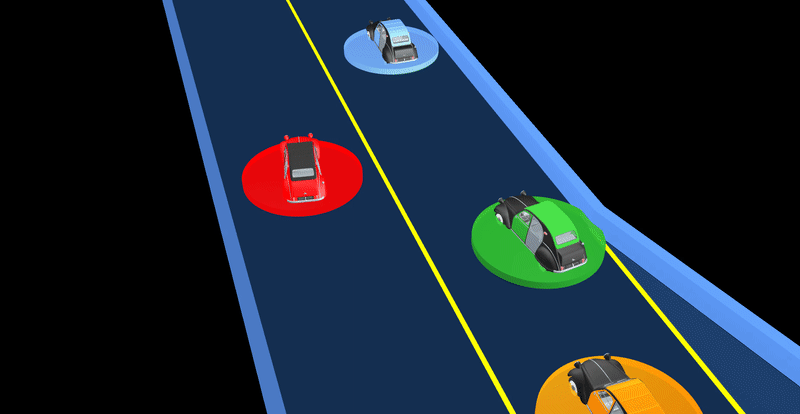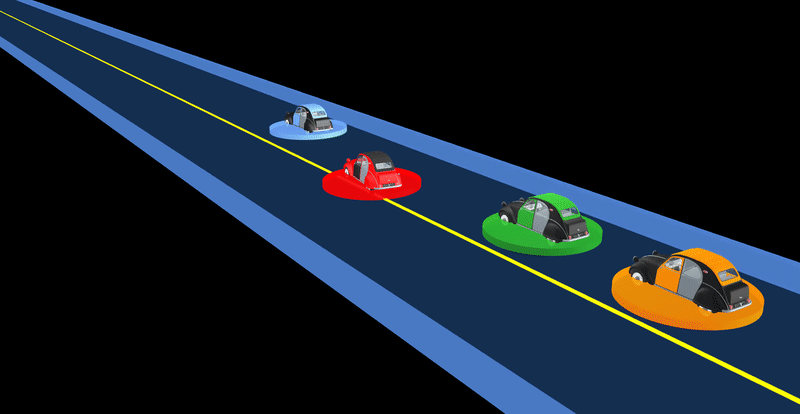
Solving Dynamic Games

We developed fast solver for constrained dynamic games and applied it to complex autonomous driving scenarios. It generates complex driving behaviors where vehicles negotiate and share the responsibility for avoiding collisions.

Computing Robustness Guarantees

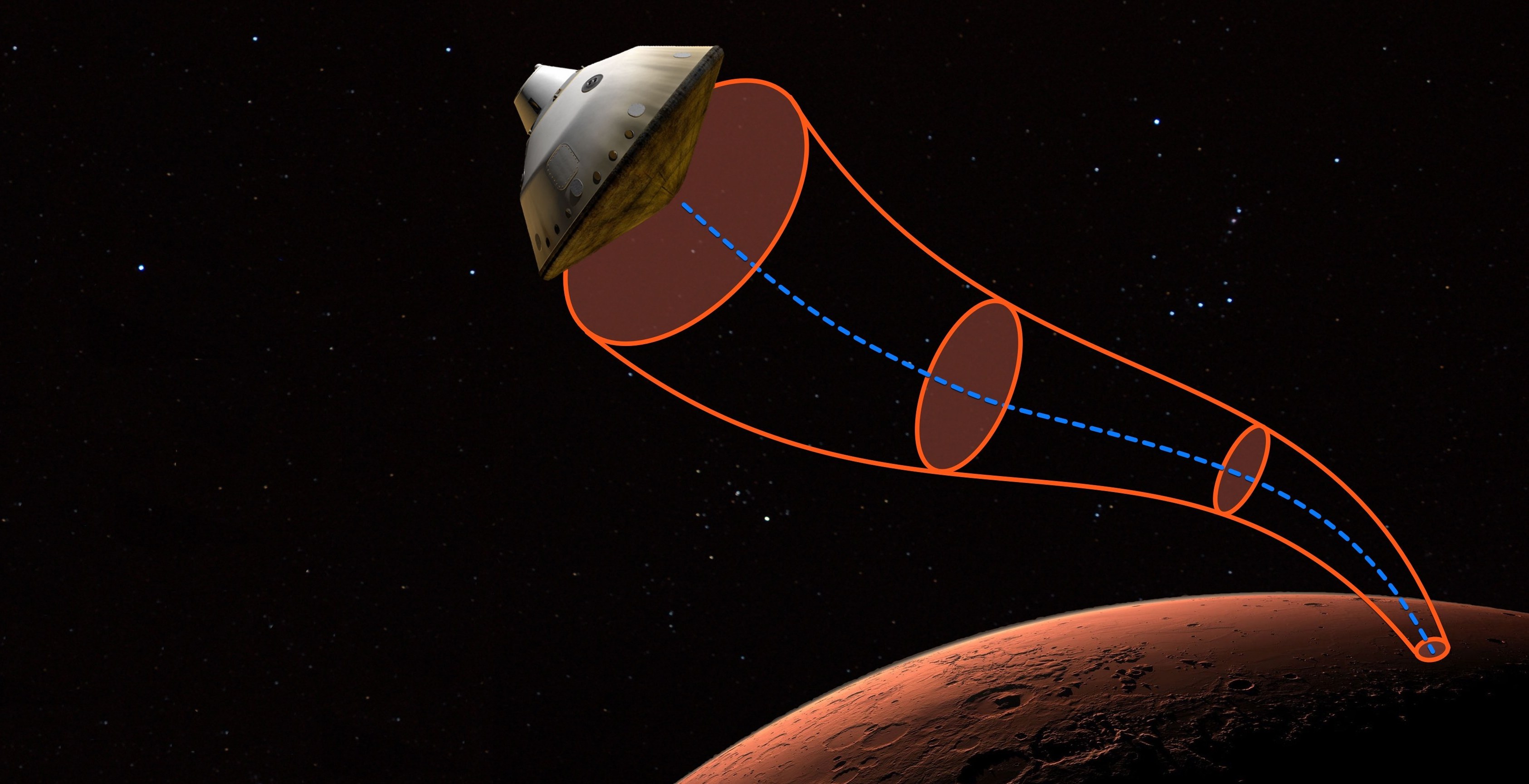
We developed an algorithm relying on a novel sampling-based technique to efficiently compute regions of finite time invariance, commonly refered to as “invariant funnels”. We apply our algorithm to a spacecraft atmospheric entry problem where the goal is to identify the landing zone that the spacecraft is guaranteed to reach under uncertain atmospheric disturbances.

Optimizing nonsmooth objective functions

We applied the Alternating Direction Method of Multipliers (ADMM) to solve optimal control problems with L1-norm cost. One application of this work is minimum-fuel trajectory optimization for satellites.